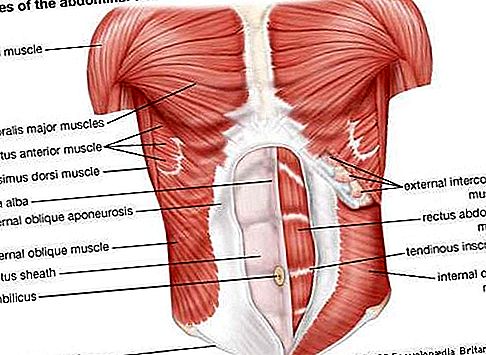
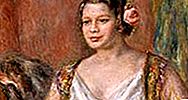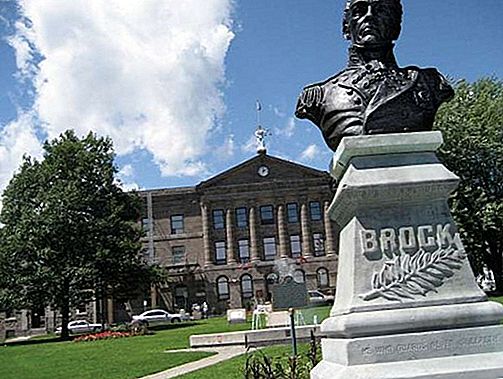Kūginis pjūvis, dar vadinamas kūgiu, geometrijoje yra bet kokia kreivė, susidaranti susikirtus plokštumai ir dešiniajam apskritam kūgiui. Priklausomai nuo plokštumos kampo kūgio atžvilgiu, sankryža yra apskritimas, elipsė, hiperbolė arba parabolė. Specialūs (išsigimę) susikirtimo atvejai būna tada, kai plokštuma kerta tik viršūnę (sukuria vieną tašką) arba per viršūnę ir kitą kūgio tašką (sukuria vieną tiesę arba dvi kertančias tieses). Žiūrėkite paveikslą.
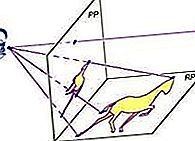
Projektyvioji geometrija: Projekciniai kūginiai pjūviai
Kūginis pjūvis gali būti laikomas dešiniojo apskrito kūgio plokštumomis (žr. Paveikslą). Atsižvelgiant į
Pagrindinius kūginių pjūvių aprašymus, bet ne pavadinimus, galima atsekti iki Menaechmuso (suklestėjo apie 350 bc), kuris yra ir Platono, ir Cnidus Eudoxus mokinys. Pergos Apolonijus (apie 262–190 bc), žinomas kaip „Didysis geometras“, kūgiškoms dalims suteikė jų pavadinimus ir pirmasis apibrėžė dvi hiperbolės šakas (kurios suponuoja dvigubą kūgį). Apolonijaus aštuonių tomų kūginių pjūvių traktatas „Kūgiai“ yra vienas didžiausių senovės pasaulio darbų.
Analitinis apibrėžimas
Kūgiai taip pat gali būti apibūdinami kaip plokštumos kreivės, kurios yra taško, judančio taip, kad atstumas nuo fiksuoto taško (fokuso) iki atstumo nuo fiksuotos linijos (krypties) yra pastovus, vadinamas kreivės ekscentriškumas. Jei ekscentriškumas lygus nuliui, kreivė yra apskritimas; jei lygus vienam, parabolė; jei mažiau nei viena, elipsė; o jei didesnė nei viena - hiperbolė. Žiūrėkite paveikslą.
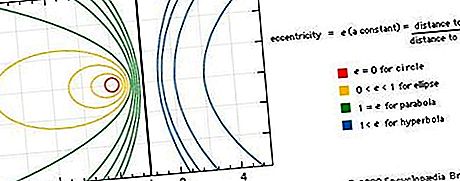
Kiekvienas kūginis pjūvis atitinka ašies formos 2 laipsnio polinominės lygties grafiką, kurio forma yra 2 + By 2 + 2Cxy + 2Dx + 2Ey + F = 0, kur x ir y yra kintamieji, o A, B, C, D, E ir F yra koeficientai, kurie priklauso nuo konkretaus kūgio. Tinkamai pasirinkus koordinatines ašis, bet kurio kūgio lygtis gali būti sumažinta iki vienos iš trijų paprastųjų r formų: x 2 / a 2 + y 2 / b 2 = 1, x 2 / a 2 - y 2 / b 2 = 1, arba y 2 = 2 taškai, atitinkamai atitinkamai elipsės, hiperbolės ir parabolės. (Elipsė, kurioje a = b iš tikrųjų yra apskritimas.) René Descartes'as (1596–1650) sukūrė platų koordinačių sistemų naudojimą algebrinei geometrinių kreivių analizei. Žr. „Geometrijos istorija: Dekarto geometrija“.
Graikų kilmė
Ankstyvoji kūginių pjūvių istorija yra susijusi su „kubo dvigubinimo“ problema. Anot Kirėno Eratostheneso (apie 276–190 bc), Delos žmonės kreipėsi į Apolono oraklą, norėdami padėti nutraukti marą (apie 430 bc), ir jiems buvo pavesta pastatyti naują „Apollo“ aukurą, kurio tūris dvigubai didesnis nei senojo aukuro. ir su ta pačia kubine forma. Sumišęs Deliansas konsultavosi su Platonu, kuris teigė, kad „orakulas reiškė ne tai, kad dievas nori dvigubai didesnio aukuro, bet kad jis, norėdamas jiems kelti užduotį, norėjo sugėdinti graikus už matematikos aplaidumą ir panieką. geometrijai. “ Chioso Hipokratas (maždaug 470–410 bc) pirmiausia atrado, kad „Deliano problemą“ galima sumažinti iki dviejų vidutinių proporcijų tarp a ir 2a (atitinkamų altorių tūrio) radimo, tai yra, nustatant x ir y taip, kad a: x = x: y = y: 2a. Tai tolygu tuo pačiu metu išspręsti bet kurias iš dviejų lygčių x 2 = ay, y 2 = 2ax ir xy = 2a 2, kurios atitinka atitinkamai dvi parabolas ir hiperbolą. Vėliau Archimedas (apie 290–211 bc) parodė, kaip kūginius pjūvius panaudoti sferai padalinti į du segmentus, turinčius tam tikrą santykį.
Diokai (apie 200 bc) geometriškai parodė, kad židinyje susitinka spinduliai, pavyzdžiui, iš saulės, kurie yra lygiagrečiai paraboloido revoliucijos ašiai (gaminami sukant parabolę aplink jos simetrijos ašį). Teigiama, kad Archimedas panaudojo šią nuosavybę priešo laivams padegti. Židinio elipsės savybes nurodė Anthemiusas iš Tralles, vienas iš Konstantinopolio Hagia Sophia katedros architektų (baigtas 537 skelbime), kaip priemonė užtikrinti, kad altorius visą dieną galėtų būti apšviečiamas saulės spindulių.